Millennium Prize Problems olarak adlandırılan ve çözülmesi için 1 milyon dolar ödül teklif edilen 8 matematik problemi.

1. Fermat's Last Theorem (çözüldü)
2. Collatz Conjecture
3. Poincaré Conjecture (çözüldü)
4. Goldbach's Conjecture
5. Birch and Swinnerton-Dyer Conjecture
6. Hodge Conjecture
7. Navier–Stokes existence and smoothness
8. Yang-Mills Existence and Mass Gap

Fermat's Last Theorem

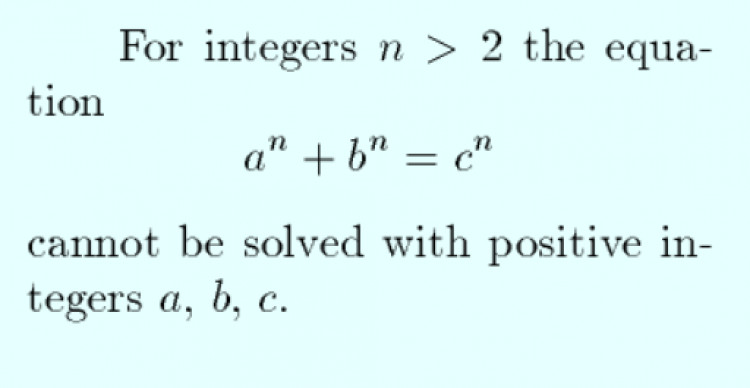
Fermat's Last Theorem, matematikçi Pierre de Fermat tarafından 1637 yılında ortaya atılan bir teoremdir. Fermat, bir notta "x^n + y^n = z^n" eşitliğinin (n > 2) hiçbir tam sayı x, y ve z için geçerli olamayacağını yazmıştır. Fermat'ın Son Teoremi olarak da bilinir, çünkü uzun süre çözülemedi ve Fermat ölmeden önce yazdığı notta eşitliğin çözümünün nasıl olduğunu açıklamamıştır. Bu teorem 1995 yılında Andrew wiles tarafından çözüldü.

Pierre de Fermat 

 

Andrew wiles

Collatz Conjecture

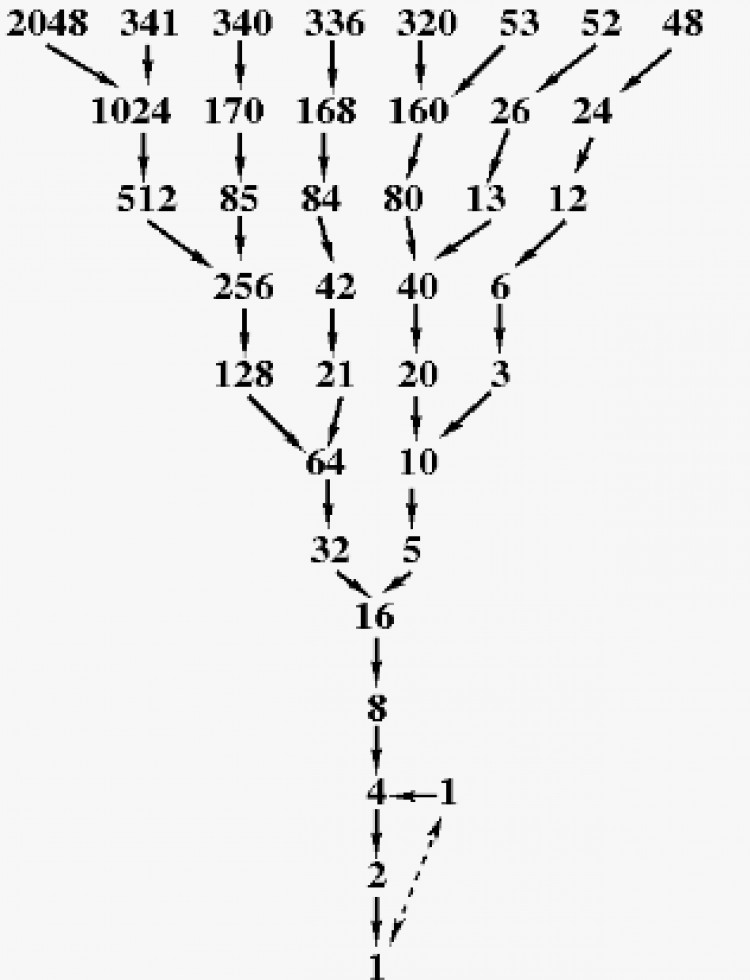
Collatz Conjecture, matematikçi Lothar Collatz tarafından 1937 yılında ortaya atılan bir kabul olarak bilinir. Bu kabul, herhangi bir pozitif tam sayı n için, n'i sırasıyla şöyle sürekli olarak işlem yaparak yeni bir sayı elde edeceğinizi söyler:

Eğer n çift ise, n / 2.
Eğer n tek ise, 3n + 1.
Collatz Conjecture'a göre, herhangi bir pozitif tam sayının uyguladığınız bu işlemlerin sonunda 1'e ulaşacak olan bir dizi oluşur. Bu kabul, çözülmemiş bir problem olarak kabul edilir ve matematik camiası tarafından hala araştırılmaktadır.

 

Lothar Collatz

Poincaré Conjecture

Poincaré Conjecture, Fransız matematikçi Henri Poincaré tarafından 1904 yılında ortaya atılan bir kabul olarak bilinir. Bu kabul, herhangi bir sınırsız küçük boyutlu, yuvarlak ve homojen 3 boyutlu uzayın (yani, her yerinde aynı yapıya sahip olan) sonlu boyutlu bir kesinin, sadece 3 boyutlu kürelerin kesimleri olabileceğini öne sürer. Poincaré Conjecture, çözülmemiş bir problem olarak kabul edilir ve matematik camiası tarafından hala araştırılmaktadır. 2002 yılında Rus matematikçi Grigori Perelman tarafından çözüldü ve Poincaré Conjecture poincaré ödülünü kazandı.

 Henri Poincaré

Grigori Perelman

Goldbach's Conjecture

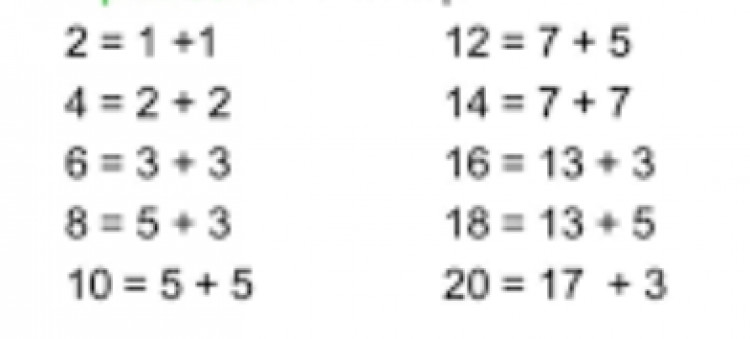
Goldbach'ın Tahmini, sayı teorisinde çözülmemiş ünlü bir problemdir. Her çift sayının iki asal sayının toplamı olarak ifade edilebileceğini iddia eder. Örneğin, 10 sayısı 3 ve 7 (ikisi de asal sayılar) toplamı olarak veya 5 ve 5 (5 asal sayıdır) toplamı olarak ifade edilebilir. Çok sayıda çalışma yapmasına rağmen, tahminin doğru veya yanlış olduğunu kanıtlayan ya da çürüten kimse bulunamamıştır.

Christian Goldbach

Birch and Swinnerton-Dyer Conjecture

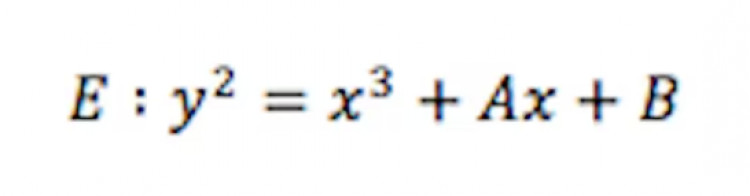
Birch ve Swinnerton-Dyer Tahmini (BSDC), eliptik eğrilerin davranışıyla ilgili matematikte çözülememiş önemli bir problemdir. John Birch ve Peter Swinnerton-Dyer tarafından 1960'larda ilk olarak önerilmesinden dolayı adını almıştır.

Tahmin, rasyonel sayılar üzerinde bir eliptik eğrinin rasyonel noktalar grubunun sıralamasının L-fonksiyonu ile yakından ilgili olduğunu öne sürer. L-fonksiyonu, eğrinin sayı teorik özelliklerini kodlayan karmaşık bir fonksiyondur. Özellikle, tahmin, rasyonel noktalar grubunun sıralamasının L-fonksiyonunun 1 noktasında sıfırın siparişi ile eşit olduğunu öngörür.

BSDC, matematikte önemli bir açık sorudur ve birçok yıldır geniş çapta incelenmiştir ancak henüz bir kanıt veya çelişki örneği bulunamamıştır. Matematikte çözülememiş en önemli problemlerden birisidir.

 

   Peter Swinnerton-Dyer

Hodge Conjecture

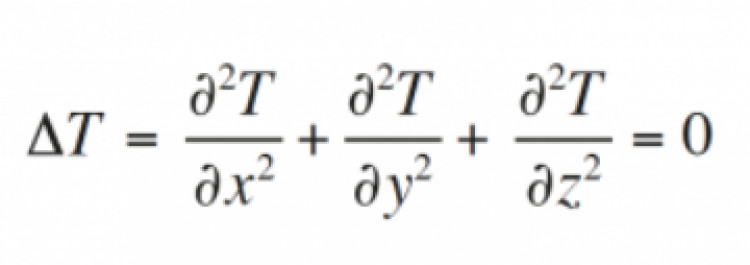
Hodge Tahmini, matematikte kompleks geometri konusunda çözülememiş önemli bir problemdir. İlk olarak 1950'lerde William Vallance Douglas Hodge tarafından ortaya atılmıştır.

Tahmin, kompleks bir varyetenin (yani kompleks sayılar üzerinde bir geometrik nesnenin) Hodge teorisi tarafından tanımlanan Hodge diamond'ının diyagonal elemanlarının sadece Hodge kalıplarından oluştuğunu öngörür. Hodge kalıpları, varyetenin homolojik özelliklerini tanımlayan matematiksel nesnelerdir.

Hodge Tahmini hala çözülmemiştir ve matematikte önemli bir açık sorudur. Çalışmalarının yanı sıra çok sayıda yan tahmini de içermektedir.

   William Vallance Douglas Hodge

Navier–Stokes existence and smoothness

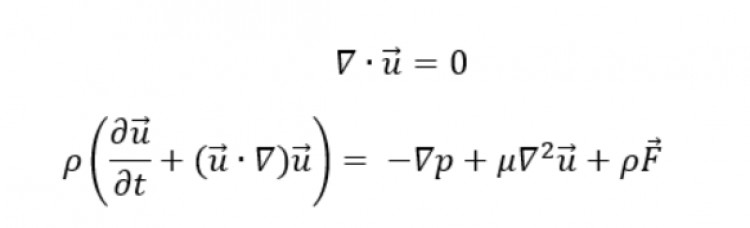
Navier-Stokes Varlık ve Pürüzlülük, matematikte mekaniğe ve mühendisliğe dayalı bir problemdir. Bu problem, Navier-Stokes denklemleri adı verilen denklemler aracılığıyla tanımlanır. Bu denklemler, bir fluidin hareketini tanımlayan matematiksel modellerdir ve genellikle gaz veya sıvıların hareketini açıklamak için kullanılır.

Navier-Stokes Varlık ve Pürüzlülük problemi, bu denklemlerin çözümlerinin varlığını ve pürüzlülüğünü (yani sürekli ve düzgün olmasını) kanıtlamak için ortaya atılmıştır. Bu problem, matematikte önemli bir açık sorudur ve hala çözülememiştir. Çözümünü bulmak, çeşitli alanlarda önemli uygulamalara yol açabilir, örneğin türbinlerin, jet motorların veya akışkanların hareketinin daha iyi anlaşılması.

George Gabriel Stokes  

Jean-Claude-Charles Navier

Yang-Mills Existence and Mass Gap

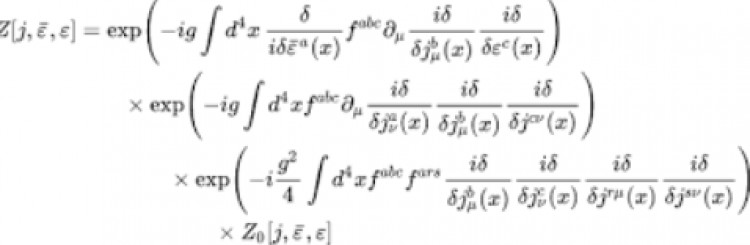
Yang-Mills Varlık ve Kütle Boşluğu, matematiksel fizikte belirli türlerde ölçek teorilerinin davranışıyla ilgili bir sorunudur. Yang-Mills denklemleri, bir kutup teorisi olarak bilinen bir fizik modelini tanımlayan denklemlerdir. Bu denklemler, güçlü etkileşimleri açıklamak için kullanılır.

Varlık ve Kütle Boşluğu problemi, Yang-Mills denklemlerinin çözümlerinin varlığını ve kütle boşluğu (yani en düşük kütleli uyumlu parçacıkların varlığını) kanıtlamak için ortaya atılmıştır. Bu problem hala çözülememiştir ve çok sayıda matematikçi ve fizikçi tarafından çalışılmaktadır. Çözümü, güçlü etkileşimlerin daha iyi anlaşılmasına ve Standard Model fiziğinde daha doğru tahminler yapılmasına yol açabilir.

Chen Ning Yang    

Robert L. Mills